All that can go wrong with recirculation
Posted: Sat Jul 05, 2008 10:30 pm
Whatever the sins of cusp confinement, it seems popular to absolve them by invoking recirculation. I see this concept to be just as weak as whiffle ball confinement. Remember that the particles are coming out from a very small spot and/or in a very narrow cone. Recirculation requires that this special flux tube and/or velocity distribution match up with the special flux tube and/or velocity distribution that would allow the particles to come back in another place. If these special conditions are met, then anything that jostles them along the way will destroy the special conditions and the particles will be trapped out in the cold.
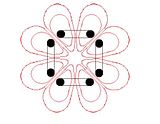
But first, do we expect the field lines of one cusp to map to the field line of another cusp? As a matter of fact, we do. There is not much that is easy to understand and express about the 3-d magnetic geometry of a polywell, but one of those things is that the field lines passing through the middles of the faces, sides, and corners of the cube are straight as an arrow. They penetrate all the way to the zero-field middle of the cube (which makes them cusps) where they intersect, and they extend all the way to infinity on the outside, where (mathematically) they also intersect. Oops. Is that what we wanted? A field line near one cusp will return to a point near another cusp, but it will take the long way around to get there, usually running into the containment vessel before it has a chance to recirculate.
And while we're talking about running into things, we all agree we want to push to the highest field technically possible, both for good confinement and high power density. This implies a some hefty magnet coils, to provide conductor cross section, to provide cooling, and to provide mechanical support against magnetic forces, and the feeds for these coils must be equally hefty for the same reasons. Why shouldn't I expect several percent of the plasma fan leaving a cusp to run into these feeds?
But we're not finished yet. Suppose we've got a flux tube that leaves one cusp and enters another without hitting anything inbetween. Will the plasma really follow it? Any electric fields - and they are postulated by the concept to be large - will shift the plasma off the flux tube through the EXB (E cross B) drift. Isn't it likely to land next to the tiny hole it was aiming for instead of in it? There are also the grad B and curvature drifts. Again, the magnetic field gradients and curvature will definitely be large. These are especially evil because they act in opposite directions for positively and negatively charge particles, leading to charge separation and a powerful EXB drift again. This is where the "bad curvature" of the magnetic field raises its head, the one that proponents are so proud that the polywell, in contrast to the evil tokamak, does not have. Well, the curvature inside the coil system is all good, but the curvature outside is all bad, and it will wreak havoc with your recirculation.
Rick Nebel is going to come back and explain that the idea of recirculation along flux loops is passe, that the current thinking is that most electrons will be turned around by the electric field between the magrid and the housing and be recirculated through the same cusp they came out of. If that happens, it will quantitatively reduce the effects I list, but not eliminate them. All these things will still be going on for the duration of the particles' excursion out of the cusp. But in fact there is no reason to expect such a local recirculation. The charge on the coils, if it is not hidden entirely by a Debye sheath, will result in an electric field at right angles to the magnetic field. There's that EXB drift again. In any self-respecting plasma, the free and easy motion of charges parallel to B will (nearly) eliminate the E field in that direction. There is also a contradiction is the idea of using the radial electric field to confine electrons *and* ions. If the field recycles electrons at some location, then it will spit out ions there, and vice versa.
This should do for a start. I believe the true believers talk about getting recirculation factors of 1000 or 10,000 (because that is what they need to compensate for the poor cusp confinement, which I argue is even poorer than they think). I can't imagine getting more than a factor of 10 (although this is hard to quantify), and I suspect you will actually get much less than that.
But first, do we expect the field lines of one cusp to map to the field line of another cusp? As a matter of fact, we do. There is not much that is easy to understand and express about the 3-d magnetic geometry of a polywell, but one of those things is that the field lines passing through the middles of the faces, sides, and corners of the cube are straight as an arrow. They penetrate all the way to the zero-field middle of the cube (which makes them cusps) where they intersect, and they extend all the way to infinity on the outside, where (mathematically) they also intersect. Oops. Is that what we wanted? A field line near one cusp will return to a point near another cusp, but it will take the long way around to get there, usually running into the containment vessel before it has a chance to recirculate.
And while we're talking about running into things, we all agree we want to push to the highest field technically possible, both for good confinement and high power density. This implies a some hefty magnet coils, to provide conductor cross section, to provide cooling, and to provide mechanical support against magnetic forces, and the feeds for these coils must be equally hefty for the same reasons. Why shouldn't I expect several percent of the plasma fan leaving a cusp to run into these feeds?
But we're not finished yet. Suppose we've got a flux tube that leaves one cusp and enters another without hitting anything inbetween. Will the plasma really follow it? Any electric fields - and they are postulated by the concept to be large - will shift the plasma off the flux tube through the EXB (E cross B) drift. Isn't it likely to land next to the tiny hole it was aiming for instead of in it? There are also the grad B and curvature drifts. Again, the magnetic field gradients and curvature will definitely be large. These are especially evil because they act in opposite directions for positively and negatively charge particles, leading to charge separation and a powerful EXB drift again. This is where the "bad curvature" of the magnetic field raises its head, the one that proponents are so proud that the polywell, in contrast to the evil tokamak, does not have. Well, the curvature inside the coil system is all good, but the curvature outside is all bad, and it will wreak havoc with your recirculation.
Rick Nebel is going to come back and explain that the idea of recirculation along flux loops is passe, that the current thinking is that most electrons will be turned around by the electric field between the magrid and the housing and be recirculated through the same cusp they came out of. If that happens, it will quantitatively reduce the effects I list, but not eliminate them. All these things will still be going on for the duration of the particles' excursion out of the cusp. But in fact there is no reason to expect such a local recirculation. The charge on the coils, if it is not hidden entirely by a Debye sheath, will result in an electric field at right angles to the magnetic field. There's that EXB drift again. In any self-respecting plasma, the free and easy motion of charges parallel to B will (nearly) eliminate the E field in that direction. There is also a contradiction is the idea of using the radial electric field to confine electrons *and* ions. If the field recycles electrons at some location, then it will spit out ions there, and vice versa.
This should do for a start. I believe the true believers talk about getting recirculation factors of 1000 or 10,000 (because that is what they need to compensate for the poor cusp confinement, which I argue is even poorer than they think). I can't imagine getting more than a factor of 10 (although this is hard to quantify), and I suspect you will actually get much less than that.